数学Ⅱ¶
1. 点と線¶
1.1. 内分と外分¶
- aとbをm:nに内分する点
\[
\frac{n \times a + m \times b}{m+n}
\]
- aとbをm:nに外分する点
\[
\frac{- n \times a + m \times b}{m - n}
\]
1.2. 2点間の距離¶
- (x1,y1), (x2, y2)の距離 ※三平方の定理を使う
\[
AB = \sqrt{(x2-x1)^2 + (y2-y1)^2}
\]
- 内分点
\[
(\frac{n \times x1 + m \times x2}{m+n}), (\frac{n \times y1 + m \times y2}{m+n})
\]
- 外分点
\[
(\frac{-n \times x1 + m \times x2}{m-n}), (\frac{-n \times y1 + m \times y2}{m-n})
\]
1.3. 三角形の重心¶
-
A(x1,y1), B(x2, y2), C(x3, y3)の重心
-
BとCの中点M(1:1に内分する座標)を求める
\[
(\frac{1 \times x2 + 1 \times x3}{1+1}), (\frac{1 \times y2 + 1 \times y3}{1+1})
\]
↓
\[
(\frac{x2 + x3}{2}), (\frac{y2 + y3}{2})
\]
- AとMを2:1に内分する点(重心)を求める
\[
(\frac{1 \times x1 + 2 \times \frac{x2 + x3}{2}}{2+1})
\]
- 2を計算した結果
\[
(\frac{x1 + x2 + x3}{3}), (\frac{y1 + y2 + y3}{3})
\]
1.4. 点と直線の方式¶
P(x1,y1)と直線(ax + by + c =0)の距離dは
\[
d = \frac{|a \times x1 + b \times y1 + c|}{\sqrt{a^2 + b^2}}
\]
2. 円の方程式¶
- 点(a,b)を中心とする半径が r の円の方程式は
\[
(x^{2} - a) + (y^{2} - b) = r^{2}
\]
\[
x^{2} + y^{2} = r^{2}
\]
- 円 x2 + y2 = r 2 上の点(x1 ,y1)における接線の方程式は
\[
x \times x1 + y \times y1 = r^2
\]
3. 三角関数¶
3.1. 基本¶
- 単位円
\[
\sin{\theta} = \frac{y}{r}
\]
\[
\cos{\theta} = \frac{x}{r}
\]
\[
\tan{\theta} = \frac{x}{y}
\]
\[
\cot{\theta} = \frac{y}{x}
\]
- 変換
\[
\sin^{2}{\theta} + \cos^{2}{\theta} = 1
\]
\[
\tan{\theta} = \frac{sin{\theta}}{cos{\theta}}
\]
\[
\cot{\theta} = \frac{cos{\theta}}{sin{\theta}}
\]
\[
\tan^{2}{\theta} + 1 = \frac{1}{cos^{2}{\theta}}
\]
- sinはy座標なので、x軸を挟んで符号が変わる
\[
\sin{(- \theta)} = -sin{\theta}
\]
- cosはy座標なので、x軸に対象
\[
\cos{(- \theta)} = cos{\theta}
\]
\[
\sin{(\theta + \frac{\pi}{2})} = cos{\theta}
\]
\[
\cos{(\theta + \frac{\pi}{2})} = -sin{\theta}
\]
- π移動する(三角関数の波を180度進めるイメージで考える)
\[
\sin{(\theta + \pi)} = -sin{\theta}
\]
\[
\cos{(\theta + \pi)} = -cos{\theta}
\]
3.2. 加法定理¶
3.2.1. 正弦(sin)・余弦(cos)の加法定理¶
\[
\sin(\alpha + \beta) = \sin{\alpha} \cdot \cos{\beta} + \cos{\alpha} \cdot \sin{\beta}
\]
\[
\sin(\alpha + \beta) = \sin{\alpha} \cdot \cos{\beta} - \cos{\alpha} \cdot \sin{\beta}
\]
\[
\cos(\alpha + \beta) = \cos{\alpha} \cdot \cos{\beta} - \sin{\alpha} \cdot \sin{\beta}
\]
\[
\cos(\alpha - \beta) = \cos{\alpha} \cdot \cos{\beta} + \sin{\alpha} \cdot \sin{\beta}
\]
3.2.2. 正接(tan)の加法定理¶
\[
\tan(\alpha + \beta) = \frac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha} \cdot \tan{\beta} }
\]
\[
\tan(\alpha - \beta) = \frac{\tan{\alpha} - \tan{\beta}}{1 + \tan{\alpha} \cdot \tan{\beta} }
\]
3.3. 倍角・半角¶
3.3.1. 2倍角の公式¶
- sin2θの公式
\[
\sin{2\alpha} = 2 \cdot \sin{\alpha} \cdot \cos{\alpha}
\]
\[
\sin(\alpha + \alpha) = \sin{\alpha} \cdot \cos{\alpha} + \cos{\alpha} \cdot \sin{\alpha}
\]
- cos2θの公式
\[
\cos{2\alpha} = \cos^2{\alpha} - \sin^2{\alpha}
\]
\[
\cos{2\alpha} = \cos^2{\alpha} - (1 - \cos^{2}{\alpha}) = 2 \cos^{2}{\alpha} -1
\]
\[
\cos{2\alpha} = (1 - \sin^{2}{\alpha}) - \sin^2{\alpha} = 1 - 2 \sin^{2}{\alpha}
\]
\[
\cos{2\alpha} = \cos^2{\alpha} - \sin^2{\alpha}
\]
\[
\cos(\alpha + \alpha) = \cos{\alpha} \cdot \cos{\alpha} - \sin{\alpha} \cdot \sin{\alpha}
\]
3.3.2. 半角の公式¶
- sinθの半角
\[
\sin^2{\frac{\theta}{2}} = \frac{1 - \cos{\theta}}{2}
\]
- cosθの半角
\[
\cos^2{\frac{\theta}{2}} = \frac{1 + \cos{\theta}}{2}
\]
- tanθの半角
\[
\tan^2{\frac{\theta}{2}} = \frac{1 - \cos{\theta}}{1 + \cos{\theta}}
\]
4. 指数・対数¶
4.1. 指数¶
- 公式1
\[
\sqrt[n]{a^{n}} = (\sqrt[n]{a})^{n} = a
\]
- 公式2
\[
\sqrt[n]{a^{n}} = = a^{\frac{1}{n}}
\]
- 公式3
\[
\frac{1}{a^{n}} = a^{-n} = (\frac{1}{a})^{n}
\]
- 公式4
\[
a^{r} \times a^{n} = a^{r + n}
\]
- 公式5
\[
a^{r} \div a^{n} = a^{r - n}
\]
- 公式5 指数の入れ替えが出来る
\[
(a^{r})^{n} = a^{r \times n} = (a^{n})^{r}
\]
- 公式6 指数の入れ替えが出来る
\[
(ab)^{n} = a^{n} \times b^{n}
\]
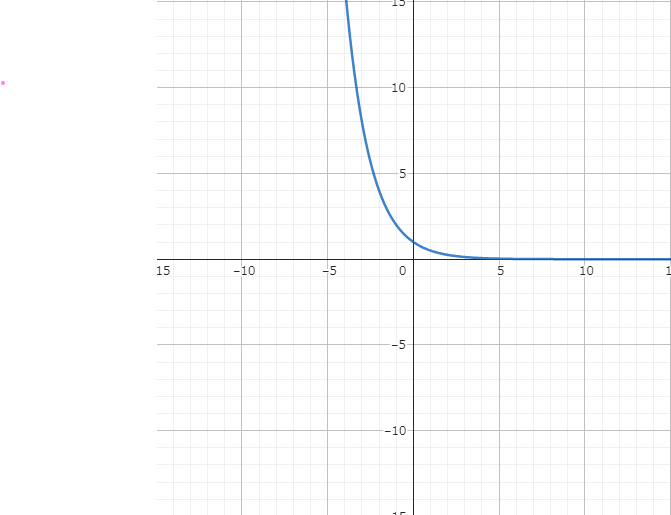
- グラフ
\[
y = 2^{x}
\]

\[
y = (\frac{1}{2})^{x}
\]
4.2. 対数¶
4.2.1. 基本¶
- 公式1
\[
\log_{a}{a^{p}} = p
\]
- 公式2
\[
\log_{a}{a^{1}} = 1
\]
- 公式3
\[
\log_{a}{1} = 0
\]
4.2.2. 基本2¶
\[
\log_{a}{M} + \log_{a}{N} = \log_{a}{M \times N}
\]
\[
\log_{a}{M} - \log_{a}{N} = \log_{a}{\frac{M}{N}}
\]
- 重要!!!
\[
\log_{a}{B} = \frac{ \log_{c}{B}}{ \log_{c}{a}}
\]
\[
\log_{a}{B} = \frac{ \log_{B}{B}}{ \log_{B}{a}} = \frac{1}{ \log_{B}{a}}
\]
\[
\log_{a}{B} = \frac{ \log_{a}{B}}{ \log_{a}{a}} = \frac{\log_{a}{B}}{ 1}
\]
- グラフ
\[
y = \log_{2}{x}
\]

\[
y = \log_{\frac{1}{2}}{x}
\]
